其它技巧

最长回文子串

少有的动态规划非最优解法的问题。

String longestPalindrome(String s) {
    String res;
    for (int i = 0; i < s.size(); i++) {
        String s1 = palindrome(s, i, i);
        //返回以s[l]和s[r]为中心的最长回文串
        String s2 = palindrome(s, i, i + 1);
        // res = longest(res, s1, s2)  
        res = res.size() > s1.size() ? res : s1;
        res = res.size() > s2.size() ? res : s2;
    }
    return res;
}

前缀和数组

如何快速得到某个⼦数组的和，主要适用的场景是原始数组不会被修改的情况下，频繁查询某个区间的累加和。

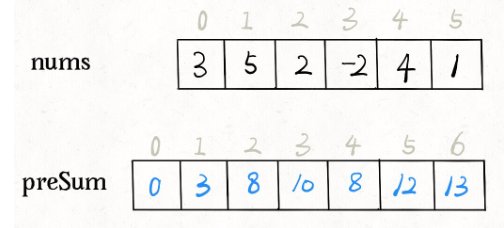
int subarraySum(int[] nums, int k) {
    int n = nums.length;
    // map：前缀和 -> 该前缀和出现的次数  
    HashMap<Integer, Integer> preSum = new HashMap<>();
    // base case  
    preSum.put(0, 1);
    int ans = 0, sum0_i = 0;
    for (int i = 0; i < n; i++) {
        sum0_i += nums[i];
        // 这是我们想找的前缀和 nums[0..j]  
        int sum0_j = sum0_i - k;
        // 如果前⾯有这个前缀和，则直接更新答案  
        if (preSum.containsKey(sum0_j))  
            ans += preSum.get(sum0_j);
        // 把前缀和 nums[0..i] 加⼊并记录出现次数  
        preSum.put(sum0_i,  
            preSum.getOrDefault(sum0_i, 0) + 1);
    }
    return ans;
}

差分数组

主要适用场景是频繁对原始数组的某个区间的元素进行增减。 比如说，我给你输入一个数组nums，然后又要求给区间nums[2..6]全部加 1，再给nums[3..9]全部减 3，再给nums[0..4]全部加 2，再给… 一通操作猛如虎，然后问你，最后nums数组的值是什么？ 构造一个diff差分数组：diff[i]=nums[i]-nums[i-1]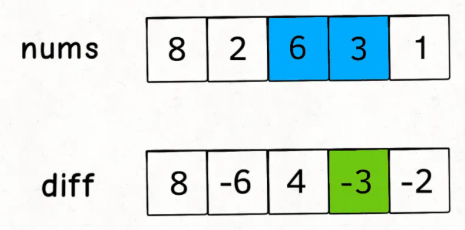： diff差分数组反推原始数组nums：nums[i]=nums[i-1]+diff[i]。

int[] nums = new int[diff.length];
// 根据差分数组反推结果数组  
nums[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
    nums[i] = nums[i - 1] + diff[i];
}

如果你想对区间nums[i..j]的元素全部加 3，那么只需要让diff[i] += 3，然后再让diff[j+1] -= 3即可：

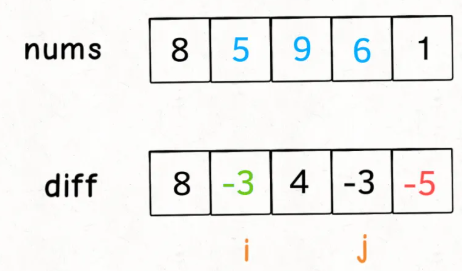
diff[i] += val;
if (j + 1 < diff.length) {
    diff[j + 1] -= val;
}

【力扣第 1109 题】「航班预订统计」

int[] corpFlightBookings(int[][] bookings, int n) {
    // nums 初始化为全 0  
    int[] nums = new int[n];
    // 构造差分解法  
    Difference df = new Difference(nums);
    for (int[] booking : bookings) {
        // 注意转成数组索引要减一哦  
        int i = booking[0] - 1;
        int j = booking[1] - 1;
        int val = booking[2];
        // 对区间 nums[i..j] 增加 val  
        df.increment(i, j, val);
    }
    // 返回最终的结果数组  
    return df.result();
}

2Sum

vector<vector<int>> twoSumTarget(vector<int>& nums, int target) {
    // nums 数组必须有序  
    sort(nums.begin(), nums.end());
    int lo = 0, hi = nums.size() - 1;
    vector<vector<int>> res;
    while (lo < hi) {
        int sum = nums[lo] + nums[hi];
        int left = nums[lo], right = nums[hi];
        if (sum < target) {
            while (lo < hi && nums[lo] == left) lo++;
        } else if (sum > target) {
            while (lo < hi && nums[hi] == right) hi--;
        } else {
            res.push_back({
                left, right
            }
            );
            while (lo < hi && nums[lo] == left) lo++;
            while (lo < hi && nums[hi] == right) hi--;
        }
    }
    return res;
}

田忌赛马

\870. 优势洗牌 打得过就打，打不过就拿自己的垃圾和对方的精锐互换。 根据这个思路，我们需要对两个数组排序，但是nums2中元素的顺序不能改变，因为计算结果的顺序依赖nums2的顺序，所以不能直接对nums2进行排序，而是利用其他数据结构来辅助。

int[] advantageCount(int[] nums1, int[] nums2) {
    int n = nums1.length;
    // 给 nums2 降序排序  
    PriorityQueue<int[]> maxpq = new PriorityQueue<>(  
        (int[] pair1, int[] pair2) -> {
        return pair2[1] - pair1[1];
    });
    for (int i = 0; i < n; i++) {
        maxpq.offer(new int[]{i, nums2[i]});
    }
    // 给 nums1 升序排序  
    Arrays.sort(nums1);
    // nums1[left] 是最小值，nums1[right] 是最大值  
    int left = 0, right = n - 1;
    int[] res = new int[n];
    while (!maxpq.isEmpty()) {
        int[] pair = maxpq.poll();
        // maxval 是 nums2 中的最大值，i 是对应索引  
        int i = pair[0], maxval = pair[1];
        if (maxval < nums1[right]) {
            // 如果 nums1[right] 能胜过 maxval，那就自己上  
            res[i] = nums1[right];
            right--;
        } else {
            // 否则用最小值混一下，养精蓄锐  
            res[i] = nums1[left];
            left++;
        }
    }
    return res;
}